Este artigo foi desenvolvido por Willian de Castro Toledo.
1. INTRODUÇÃO
Estimar a vida útil de uma correia transportadora de forma assertiva é complexo devido às variáveis operacionais que podem afetar seu desempenho, mas é de grande importância para as empresas ter esta informação para obter melhor planejamento e confiabilidade nas operações, a fim de fazer as substituições no momento certo, além de manter níveis de estoques adequados.
Menezes et al [1] dizem que os custos envolvidos de aquisição e na operação de sistemas por correias transportadoras são os mais relevantes na industria mineral, e apesar disto, ainda é comum que as decisões relacionadas as substituições sejam feitas sem critérios bem estabelecidos, em geral de forma subjetiva baseada na experiência da equipe técnica, no próprio histórico de vida útil ou por alguma técnica de monitoramento.
Alguns trabalhos já foram desenvolvidos sobre este assunto, com destaque para o trabalho de Pitcher [2] que desenvolveu uma fórmula matemática para estimar a vida útil de uma correia transportadora baseado nas principais variáveis do processo operacional, mas o autor ressalta que o método tem que ser usado apenas para prever a espessura da correia e como ferramenta para otimizar o regime de carga durante o ciclo de vida em fase de projeto, portanto o método é limitado para aplicar em casos reais de operação.
Veloso [3] elaborou uma modelagem da degradação de correias transportadoras utilizadas em função do tempo de outras variáveis independentes que fazem parte do processo de mineração e que influenciam no desgaste das correias. O trabalho resultou em potencial ganho financeiro em função da diferença da vida útil das correias que era praticado pela equipe e pela vida útil calculada pelos modelos matemáticos.
Jurdziak e Hardygora [4] modelaram o tempo de vida útil de uma correia transportadora com uso da distribuição de Weibull que teve resultados satisfatórios, porém os autores utilizaram como dados de entrada os tempos até a falha baseados em históricos e não levaram em consideração os mecanismos de falhas presentes em um caso real de operação.
Neste contexto, percebe-se ainda grande oportunidade de melhoria na previsibilidade de vida útil das correias transportadoras, contudo, este trabalho tem o proposito de demonstrar a estimativa de vida útil por regressão linear simples através da degradação real da cobertura superior da correia pelo controle e monitoramento de ultrassom e determinar as curvas de confiabilidade e risco pela distribuição de Weibull.
2. REFERENCIAL TEÓRICO
2.1 Correia transportadora
Correia transportadora é definida pela ABNT [5] como equipamento “contínua ou sem-fim, destinada a formar a superfície de sustentação sobre a qual será assentado o material a ser transportado. O movimento da correia produz o transporte propriamente dito”, ou seja, são equipamentos para manuseio de material a granel utilizado em grande escala principalmente no ramo de mineração. Basicamente, uma correia transportadora é composta por duas partes: a carcaça interna e as coberturas externas (superior e inferior) conforme mostra a figura 01.
- Coberturas: Tem a função de proteger a carcaça da abrasão causada pelo carregado do material ou qualquer outra condição presente no ambiente de operação que possa contribuir para a deterioração da correia transportadora.
- Carcaça: É a seção estrutural mais importante da correia transportadora, pois tem como objetivo transmitir a força necessária para elevar e mover a correia carregada e absorver a energia de impacto liberada pelo material ao ser carregado na correia através da calha de alimentação. A carcaça pode ser fabricada de lonas têxteis ou por cabos de aço.

Portanto, correia transportadora é um componente sujeito a trocas periódicas. Na correia ideal, o desgaste total da cobertura deveria coincidir com o final de vida útil da carcaça, mas normalmente as coberturas desgastam primeiro, principalmente a cobertura superior. Este desgaste quando acontece de forma normal é devido à ação abrasiva causada pelo carregamento do minério através do chute de alimentação sobre a cobertura da correia quando em movimento.
2.2 Regressão linear simples
O modelo de regressão linear simples consiste em um conjunto de métodos e técnicas para estabelecer uma equação matemática que descreve o relacionamento entre duas variáveis, ou seja, uma variável chamada de dependente estar relacionada a uma ou mais variáveis independentes por uma equação linear que normalmente é demonstrada através de uma reta. Este método é utilizado com o objetivo de prever um valor que não se consegue estimar inicialmente. Para se obter o cálculo da equação da reta, basta aplicar a seguinte equação 01:

Na equação 01, o “y” representa a variável dependente e o “x” a variável independente. O termo “a” representa à interseção da linha no eixo y e “b” a inclinação da reta conforme representação gráfica na figura 02.

Os valores de “a” e “b” podem ser calculados através das equações 02 e 03. O termo “n” corresponde ao número de amostras utilizadas no cálculo.
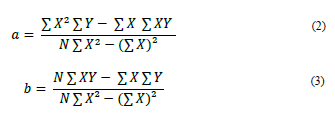
Outro fator importante no cálculo de regressão linear simples é o coeficiente de correlação “R” que indica o grau de relacionamento entre as variáveis “x” e “y” em uma amostra e mede a intensidade e direção da relação linear destas variáveis e sempre será um valor entre -1 <= R <= 1. O coeficiente de correlação “R” é calculado pela equação 04.
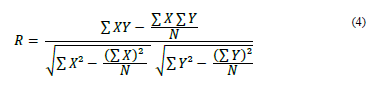
A interpretação do resultado de “R” pode ser entendida conforme figura 03.
- Quanto mais próximo de –1: maior correlação negativa;
- Quanto mais próximo de 1: maior correlação positiva;
- Quanto mais próximo de 0: menor a correlação linear;
- Igual a 0: Não existe correlação.

Montgomery e Runger [7] dizem que a primeira aplicação do termo análise de regressão foi utilizada pelo Sir. Francis Galton em um estudo realizado para avaliar a altura dos pais (variável x) com a altura dos filhos (variável y). Neste estudo, percebeu-se que os pais de estatura alta tinham em média filhos de estatura alta e pais de estatura baixa tinham em média filhos de estatura baixa, ou seja, a altura dos filhos regrediu em relação à média. Neste sentido, ele denominou regressão ao processo geral de estimar o valor de uma variável (a altura dos filhos) a partir do valor de outra (a altura dos pais).
2.3 Distribuição de Weibull
A distribuição de Weibull é uma expressão semi-empírica desenvolvida pelo físico sueco Ernest Hjalmar Wallodi Weibull, que em 1939 apresentou o modelo de planejamento estatístico sobre a fadiga dos materiais que é extensivamente usada em engenharia da confiabilidade, análise de sobrevivência e em outras áreas devido a sua versatilidade e simplicidade. A distribuição de Weibull permite:
- Representar falhas típicas de partida (mortalidade infantil), falhas aleatórias e falhas devido ao desgaste;
- Obter parâmetros significativos da configuração das falhas;
- Representação gráfica simples.
Em geral, suas aplicações visam à determinação do tempo de vida médio e da taxa de falhas em função do tempo da população analisada. Ressalta-se que o sucesso da distribuição se justifica não só pela sua eficácia, mas também pelo fato de existirem recursos gráficos que facilitam sua interpretação e por ser capaz de fazer previsões de acurácia razoável mesmo quando a quantidade de dados disponível é baixa. A distribuição de Weibull utiliza as seguintes equações 05 e 06 com os parâmetros t, η e β:
A equação 05 mostra a probabilidade de falhas F(t) de um item em um dado intervalo de tempo “t” de operação (risco).

A equação 06 mostra a probabilidade o qual um equipamento não irá falhar R(t) para um dado período de tempo “t” de operação (confiabilidade).

t: Vida mínima ou confiabilidade intrínseca (tempo de operação a partir do qual o equipamento passa a apresentar falhas, ou seja, intervalo de tempo que o equipamento não apresenta falhas).
η: Vida característica ou parâmetro de escala.
β: Fator de forma que indica a forma da curva e a característica das falhas.
β < 1 = Mortalidade infantil: falhas precoces, taxa de falha é decrescente.
β = 1 = Falhas aleatórias, taxa de falha é constante.
β > 1 = Falhas por desgaste, taxa de falha é crescente
3. ESTUDO DE CASO
A seguir serão aplicados os conceitos de regressão linear simples e distribuição de Weibull para estimar a vida útil de uma correia transportadora e determinar sua curva de confiabilidade e risco.
3.1 Controle da degradação da cobertura superior da correia transportadora
A técnica de monitoramento por ultrassom é fortemente utilizada pelo setor de manutenção para medir a espessura das coberturas da correia e acompanhar sua degradação. Em condições normais de operação, a cobertura superior sofre o maior desgaste devido à ação abrasiva causada pelo carregamento do minério e com outros componentes do transportador. Um perfil de desgaste normal é mostrado na figura 04.

Em resumo, esta técnica utiliza como principio a emissão e recebimento de ondas ultrassônicas para fazer a leitura no interior das peças que estão sendo medidas. Em correia transportadora as medições são feitas geralmente pela seção transversal (largura da correia) para medir a sua espessura conforme figura 05.

3.2 Cálculo da vida útil baseado na regressão linear simples
O cálculo da vida útil baseado na regressão linear será realizado conforme exemplo da tabela 01, que mostra o registro das medições contendo 10 pontos medidos pela seção transversal da correia transportadora em 08 datas. O controle iniciou-se em 15/01/18 com a instalação da correia transportadora nova que possui cobertura superior de 10 mm e a última medição foi realizada em 03/03/19. Para fazer uso da regressão linear em correia transportadora, é necessário definir que a variável “x” é o tempo de operação e a variável “y” são os pontos de espessura medidos.
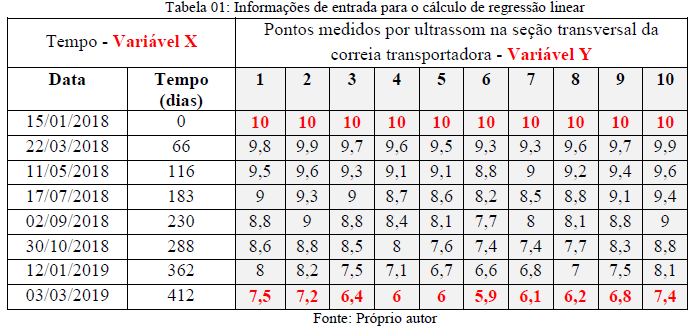
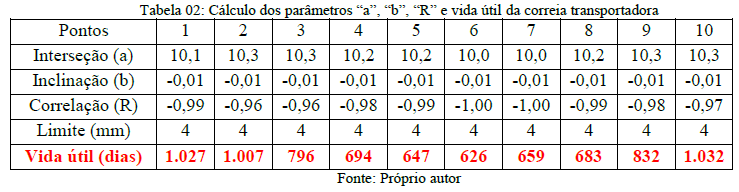
Aplicando os cálculos de regressão linear simples é possível obter os valores de interseção “a” e inclinação “b” da reta e seu coeficiente de correlação “R”. Os resultados podem ser vistos na tabela 02. Percebe-se que existe uma forte correlação negativa (valores encontrados de “R” próximos a menos 1), isto significa que as duas variáveis se movem em direções opostas, ou seja, com o aumento do tempo de operação existe a redução da espessura da correia transportadora.
Para fazer o cálculo da estimativa da vida útil é necessário definir o limite mínimo de borracha na cobertura superior conforme figura 06. Este limite fica a critério do usuário, sendo que este valor pode ser informado por fabricantes e/ou por normas. Neste exemplo foi definido como limite mínimo o valor de 4 mm, com isto, é possível calcular a vida útil conforme equação 07 e os resultados podem ser vistos na tabela 02.


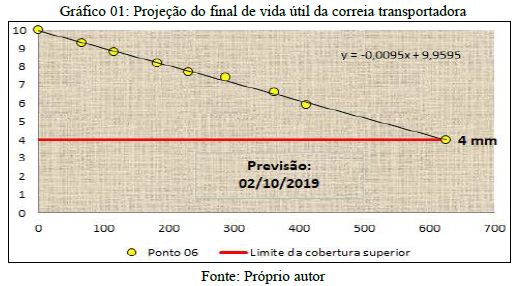
Considerando que a correia transportadora foi instalada na data de 15/01/2018 conforme mostra a tabela 01 e sua menor projeção conforme mostra a tabela 02 é de 626 dias para o ponto número 06, sua previsão para alcançar o limite de espessura da cobertura superior de 4 mm é para o dia 02/10/2019 conforme gráfico 01.
3.3 Distribuição de Weibull
O cálculo da distribuição de Weibull através da regressão linear neste trabalho tem o objetivo de determinar as curvas de confiabilidade e risco para os dados de vida útil da correia transportadora. O método possui as seguintes etapas:
1. Colocar as informações de vida útil em ordem crescente de 1 a 10;
2. Calcular a aproximação Q(t) para representar a frequência acumulada pela equação 08 de Bernard, onde “i” é a posição do dado de vida e “n” é o número total de amostras. Esta equação é utilizada para aproximação quando existe número limitado de dados.

3. Linearizar a equação 05 para a equação de uma reta Y = ax + b. Este processo é feito para converter uma curva em uma reta para facilitar a análise conforme mostrado pelas equações 09,10 e 11.
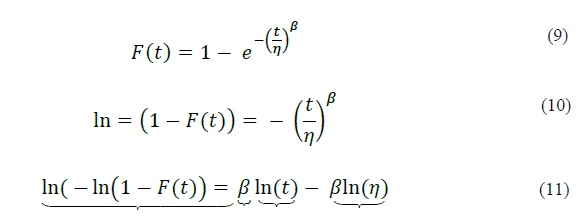
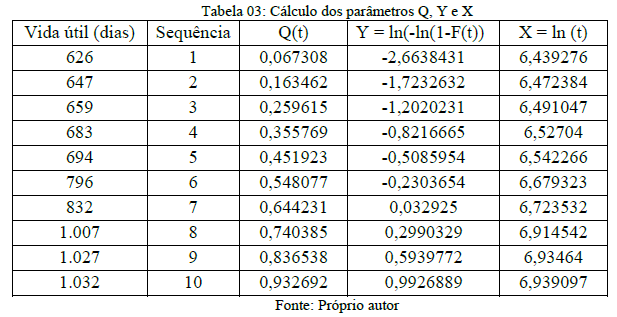
A partir dos resultados das equações 8 e 11 é possível obter a tabela 03 e aplicar a regressão linear para calcular o fator de forma “β” e o parâmetro de escala “η” através das equações 12, 13 e 14. Os resultados podem ser vistos na tabela 04.


Aplicando as equações 05 F(t) e 06 R(t) é possível obter os valores de confiabilidade e risco conforme tabela 05 e gráfico 02.
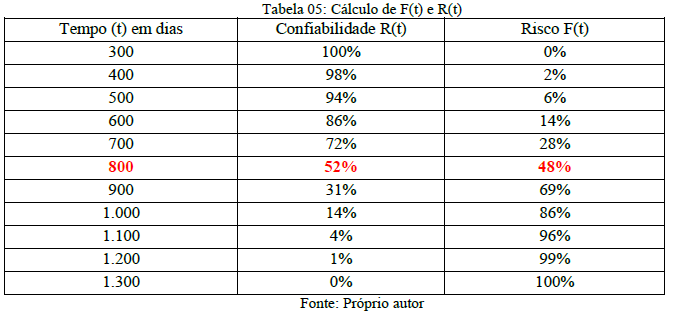
Analisando o gráfico, percebe-se que com 800 dias de operação a correia transportadora tem 52% de confiabilidade e 48% de risco em ter todos os 10 pontos medidos com espessura igual a 4 mm.
CONCLUSÃO
Neste trabalho foi mostrado uma alternativa para ajudar no acompanhamento do desgaste real de uma correia transportadora pela técnica de ultrassom. Através dos dados coletados sobre a espessura das coberturas da correia transportadora, principalmente na cobertura superior onde o desgaste é mais acelerado, é possível estimar o final de vida útil por regressão linear simples e através da distribuição de Weibull determinar as curvas de confiabilidade e risco.
No exemplo apresentado houve forte grau de correlação entre as variáveis “X” (tempo de operação) e “Y” (espessura da correia) o que indica que o método pode ser aplicado na prática, porém vale ressaltar que para este método ser assertivo é preciso manter o acompanhamento periódico das medições e coleta dos dados e a correia transportadora deve apresentar perfil de desgaste normal, ou seja, sem grandes interferências de outros mecanismos de falhas, tais como rasgos, falha nas emendas, fadiga da carcaça e etc.
Por fim, mediante a validação dos resultados na prática, é possível que este método possa servir como base para o desenvolvimento de um software para tornar os cálculos e as análises mais precisas.
REFERÊNCIAS
[1] MENEZES, I. M. DE; ALMEIDA, M. DE L.; CASTRO, C. H.; CRUZ, M. M. Tecnologias inovadoras para maximizar a vida econômica de correias transportadoras. 1° Congresso Mundial de Manutenção. Anais…, (2002).
[2] PITCHER. D. M. Design of Load Chutes for Optimum Belt Life. Dunlop África products.
[3] VELOSO, CAMPOS RICARDO. Modelagem de curvas de degradação de correias transportadoras com base em covariáveis inerentes ao processo de mineração. Programa de Pós Graduação em Engenharia de Produção. Porto Alegre, 2014.
[4] JURDZIAK, L.: HARDYGORA, M. Determination of the distribuition function of conveyor belt operating time. Mine Planning and Equipament Selection, v.37, n 6, 1997.
[5] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6177: Transportadores contínuos – Transportadores de correia – Terminologia. Brasil, ABNT. 2016.
[6] COTA, PAIVA FÁBIO. Monitoramento da espessura de correias transportadoras. UFSJ, 2010.
[7] MONTGOMERY, Douglas C.; RUNGER, George C. Estatística Aplicada e Probabilidade para Engenheiros. LTC: Rio de Janeiro, 2003.
[8] CONTISERVICES. Recuperação de correia transportadora. Disponível em: http://contiservices.com.br/servicos/recuperacao-de-correias-transportadoras/. Acesso em 05 mar 2019.
[9] OLYMPUS. Teste de espessura para esteiras rolantes com borracha reforçada. Disponível em: https://www.olympus-ims.com/pt/applications/thickness-testing-rubber-conveyor-belt/. Acesso em 05 mar 2019.